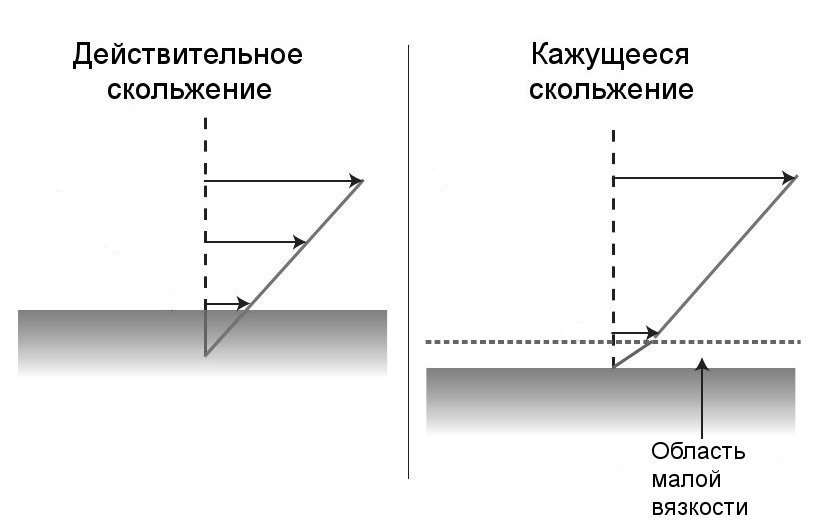
Схема кажущегося и действительного скольжения
Тем не менее, много десятков лет спустя после выхода в свет трудов Прандтля, профессора Королевского технологического института (г.Стокгольм, Швеция) К.Джонсон и Й.Хоффман предлагают определять, скажем, аэродинамическое сопротивление автомобиля, численно решая уравнения Навье-Стокса с граничным условием проскальзывания вместо условия прилипания [Hoffmann J., Johnson C. Computational Turbulent Incompressible Flow. Springer, 2007.- 397 p.]. Сама постановка вопроса звучит кощунственно, настолько привычно считать условие прилипания одним из незыблемых оснований гидродинамики.
Как сказано в одной хорошей книге, "не всегда следует пересказывать хорошо изложенную мысль своими словами и часто портить ее этим" [Кричевский И.Р. Понятия и основы термодинамики.- М.: Химия, 1970.- 440 с.]. В данном случае большая цитата из работы С.Гольдштейна не кажется неуместной [Гольштейн С. Заметка об условиях на поверхности соприкосновения жидкости с твердым телом / Современное состояние гидроаэродинамики вязкой жидкости, т.2.- М.: Государственное издательство иностранной литературы, 1948.- С.356-361]:
"Уже Даниил Бернулли сознавал, что реальная жидкость не может свободно скользить по поверхности твердого тела; этому факту он приписывал определенные большие расхождения между результатами, вычисленными им для идеальной жидкости, и результатами, которые он получил при измерении в реальной жидкости: "Наблюдаются огромные различия, главным образом в части прилипания воды к стенкам трубы; это прилипание заведомо может в некоторых случаях вызывать невероятные эффекты" [Bernoulli D. Hydrodynamica.- Argentorati, 1738.- P.59]. Дюбуа [Du Buat. Principes d'Hydraulique. Vol.1.- Paris, 1786.- Pp.92-93] пришел к заключению, что в случае, когда средняя скорость воды, текущей в канале, достаточно мала, жидкость, прилегающая к поверхности, находится в покое. Кулон нашел, что сопротивление колеблющегося в воде металлического диска мало изменялось в случае, когда диск смазывался жиром и когда жир покрывался растертым в порошок песчаником; таким образом, характер поверхности практически не оказывал влияния на сопротивление [Coulomb // Mémoires de l'Institut National des Sciences et des Arts: Sciences Mathématiques et Physiques.- 1800, Prairial an IX.- Vol.3.- P.286]; он также предположил, что молекулы жидкости, находящейся в соприкосновении с колеблющимся цилиндром, имеют скорость, одинаковую с цилиндром, что молекулы, находящиеся на небольшом расстоянии от цилиндра, имеют меньшую скорость и что на расстоянии в 2 или 3 мм их скорость становится равной нулю (цит. соч., стр.296).
В течение XIX столетия различными авторами в разное время были предложены три различных гипотезы. Согласно первой гипотезе, скорость у твердой стенки такая же, как скорость самого твердого тела, и изменяется непрерывно в жидкости, которая имеет всюду одинаковые свойства. Таково, повидимому, было мнение Кулона. Вторая гипотеза была сформулирована весьма четко Жираром в дискуссии по поводу его экспериментов с течением жидкостей в трубах. Он предположил, что весьма тонкий слой жидкости остается целиком связанным со стенками. Тогда возникает вопрос об условиях на внешней поверхности этого слоя. Жирар допустил, что остальная жидкость скользит по этому слою. Он предположил также, что в случае, если стенки всюду состоят из одного и того же материала, слой имеет постоянную толщину, так что поверхность слоя представляет для течения те же самые неправильности, как и сами стенки. Далее, он предположил, что толщина этого слоя зависит от кривизны стенки и от температуры [Girard // Mémoires de la Classe des Sciences Mathématiques et Physiques de l'Institut de France.- 1813, 1814, 1815.- Vol.14.- Pp.254, 324, 329...]. Он принимал, что эта толщина различна для различных жидкостей или различного материала стенки и что она обращается в нуль в случае жидкостей, которые не смачивают стенки, как, например, для ртути в стеклянных трубках; в таких случаях он предполагал, что жидкость скользит по поверхности [Mémoires de l'Académie Royale des Sciences de l'Institut de France.- 1816.- Vol.1.- Pp.235, 247, 258]. Третья гипотеза была предложена Навье, который на основании тех же молекулярных гипотез, которые привели его к уравнениям движения вязкой жидкости, пришел к выводу, что на твердой границе имеет место скольжение и что это скольжение встречает сопротивление силы, пропорциональной относительной скорости. Так как касательные напряжения на твердой стенке в любой точке такие же, как напряжения в соседней внутренней точке жидкости, то это эквивалентно граничному условию βu=μ∂u/∂n для течения в одном направлении вдоль плоской стенки, где u - скорость, дифференцирование производится по внешней нормали, β - постоянная, так что μ/β есть некоторая длина. Эта длина равна нулю в случае, если нет скольжения. Пользуясь этой теорией [Navier // Там же.- 1823.- Vol.6.- Pp.414-416, 432-436], Навье объяснил результаты Жирара.
В течение некоторого времени был разброд. Пуассон получил условия, по существу одинаковые с условиями Навье, но он предположил, что эти условия следует применять на внешней поверхности неподвижного или квази-твердого слоя, подобного слою Жирара [Poisson // Journal de l'École Polytechnique.- 1831.- Vol.13.- Pp.161-169; см. также Mémoires de l'Académie Royale.- 1832.- Vol.11.- P.539].
Стокс сначала склонялся в пользу первой гипотезы, но когда расчеты течения в трубах привели к результатам, расходящимся с экспериментами, ему известными (хотя они были бы в согласии с результатами Гагена или Пуазейля), он колебался между этой гипотезой и гипотезой Навье [Stokes // Trans. Camb. Phil. Soc.- 1845.- Vol.8.- Pp.299, 300; Math. and Phys. Papers.- Vol.1.- Pp.96-98]. В своем отчете Британской ассоциации в 1846 г. он упоминает о всех трех гипотезах, не высказываясь решительно в пользу какой-нибудь одной из них [Papers.- Vol.1.- Pp.185, 186]. В конце концов Стокс решает дело в пользу первой гипотезы на том основании, что наличие скольжения должно предполагать, что трение между твердым телом и жидкостью имеет иной характер и бесконечно меньше, чем трение между двумя слоями жидкости, а также и потому, что согласие с наблюдением результатов, получавшихся в предположении отсутствия скольжения, было в высшей степени удовлетворительным [Trans. Camb. Phil. Soc.- 1851.- Vol.9.- Pp.17, 18; Math. and Phys. Papers.- Vol.3.- Pp.14, 15]...
Постепенно ... гипотеза, окончательно принятая Стоксом,- что скольжения нет и что все части жидкости имеют одинаковые свойства - завоевала признание. Вычисления по этой гипотезе для случая течения в трубах, начатые Стоксом [Trans. Camb. Phil. Soc.- 1845.- Vol.8.- Pp.304, 305; Papers.- Vol.1.- Pp.104, 105] и выполненные различными авторами [Wiedemann // Poggendorff's Annalen der Physik u. Chemie.- 1856.- Vol.99.- Pp.217-221; Neumann (см. Jacobson // Archiv für Anatomie, Physiologie u. wissenschaftliche Medicin.- 1860.- Pp.88-91); Hagenbach // Poggendorff's Annalen.- 1860.- Vol.109.- Pp.385-426; Mathieu // Comptes Rendus des Séances de l'Académie des Sciences.- 1863.- Vol.57.- Pp.320-324; Boussinesq // Comptes Rendus.- 1867.- Vol.65.- Pp.46-48], дали согласные результаты не только в случаях, когда они применялись к экспериментам Пуазейля над течением воды, но также - вопреки мнению большинства этих авторов и в противоположность экспериментам, выполненным самим Пуазейлем [См. стр.1186 отчета о работе Пуазейля, составленного Араго, Бабине, Пиобером и Реньо, (Comptes Rendus.- 1842.- Vol.15.- Pp.1167-1186)],- и в случае течения ртути в стеклянных трубках (которые не смачиваются ртутью [Warburg // Poggendorff's Annalen.- 1870.- Vol.140.- Pp.367-379; Villari // Mémoire della Academia delle Scienze dell Instituto di Bologna (3).- 1875.- Vol.6.- Pp.487-520; Koch // Wiedemann's Annalen der Physik u. Chemie.- 1881.- Vol.14.- Pp.1-12)])...
Максвелл, хотя и осторожный в высказываниях и попытках исследования (так как по его словам, "всегда некоторый слой газа, ближайший к твердому телу, находится в совершенно ином состоянии, чем остальной газ"), все же произвел некоторые вычисления по требованию Комиссии королевского общества и пришел к заключению, что если нет различия температур, то скольжение происходит в согласии с уравнением Навье и длина μ/β является небольшим кратным средней длины свободного пробега L молекулы газа, вероятно, около 2L. Таким образом при атмосферном давлении скольжение было бы пренебрежимо малым; однако, для разреженных газов оно было бы значительным. Этот последний вывод находится в согласии с опытом [Maxwell // Phil. Trans.- 1879.- Vol.170.- Pp.249-256; Scientific papers.- Vol.2.- Pp.703-709]".
На сегодняшний день обзор Гольдштейна сохранил свое значение только как исторический очерк развития концепции прилипания/скольжения. Современное состояние вопроса изменилось чрезвычайно сильно, особенно за первое десятилетие XXI в., благодаря непрекращающейся миниатюризации и технологическому совершенствованию средств измерения.
За последние годы проведено много новых исследований, посвященных феномену прилипания/скольжения ньютоновских жидкостей. Среди опубликованных по этой теме работ есть и хорошие обзоры: "Микрогидродинамика: граничное условие прилипания" [Lauga E., Brenner M.P., Stone H.A. Microfluidics: The no-slip boundary condition / Springer Handbook of Experimental Fluid Mechanics (edited by Tropea C., Yarin A.L., Foss J.F.). Springer, 2007.- 1557 p.], "Скольжение на границе с твердой поверхностью в ньютоновских жидкостях: обзор экспериментальных исследований" [Neto C., Evans D.R., Bonaccurso E., Butt H.-J., Craig V.S.J., Williams D.R.M. Boundary slip in Newtonian liquids: a review of experimental studies // Rep. Prog. Phys.- 2005.- Vol.68.- P.2859-2897], "Вопросы скольжения при течении сложных жидкостей вдоль твердой поверхности" [Granick S., Zhu Y., Lee H. Slippery questions about complex fluids flowing past solids // Nature Materials.- 2003.- Vol.2.- P.221-227] и др. Не ставя целью сколько-нибудь подробно и глубоко осветить современные исследования, связанные с условием прилипания (фактически, это уже другая наука - микрогидродинамика), ограничимся взглядом на эти результаты с точки зрения обычной "макрогидродинамики".

Общепринято характеризовать проскальзывание с помощью так называемой длины скольжения λ. Этот параметр был введен еще Навье в 1823 г. и впоследствии использовался Максвеллом. Он связан со скоростью проскальзывания vs на стенке соотношением vs=λ·∂U/∂y (∂U/∂y - местное напряжение сдвига) и имеет размерность длины.
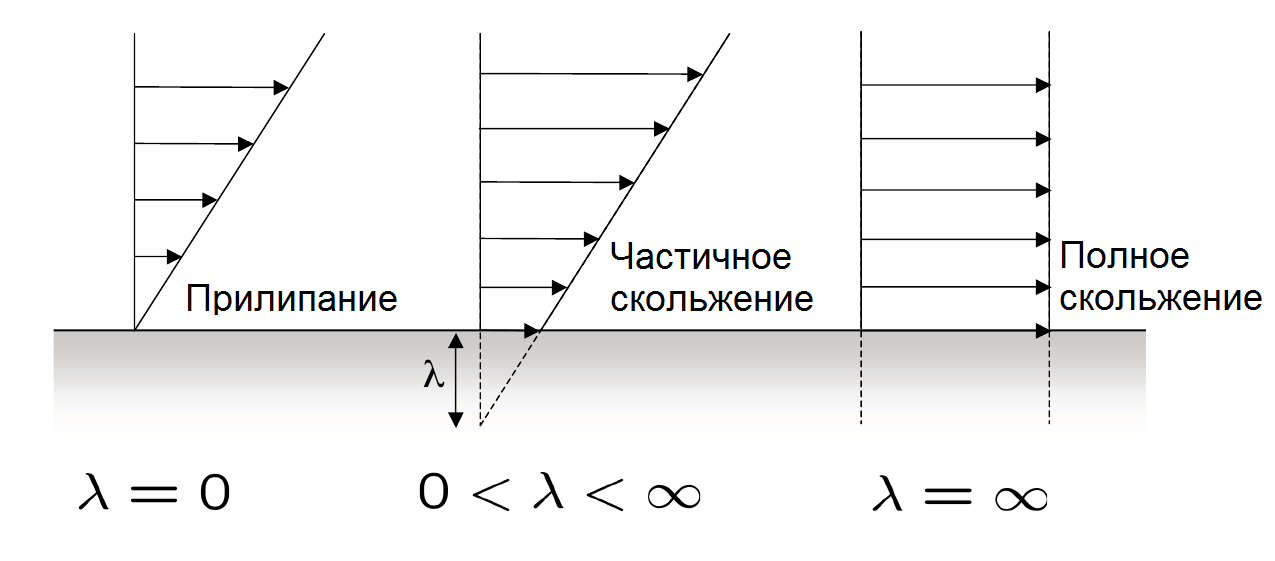
Для течения чистого сдвига λ может быть истолковано как фиктивное расстояние от поверхности до точки, где экстраполированная внутрь твердого тела скорость скольжения становится равной нулю.
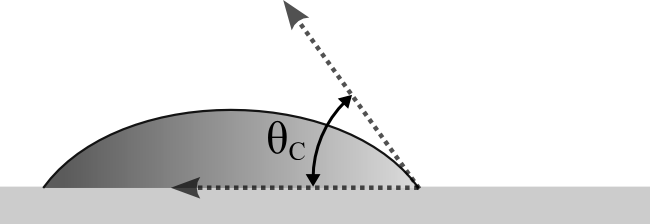
Угол контакта θC, характеризующий смачиваемость поверхности жидкостью,- это угол, который образует жидкость с твердой поверхностью в точке контакта трех фаз. Принято разделять поверхности на:
Во многих практических расчетах принимают, что абсолютная величина шероховатости внутренней поверхности трубы равна 0.05 мм = 50000 нм [Menon E.S. Piping Calculations Manual.- McGraw-Hill Companies, 2005.- 666 p.]. А до какого предела можно уменьшить размер шероховатости? Для эталонного измерения числа Авогадро в австралийском Центре высокоточной оптики были изготовлены две сферы из изотопа кремний-28 с размером неровностей на них не более 97 нм. Размер молекулы кислорода (если считать для простоты, что она имеет форму куба) - порядка 0.33 нм [Buyana T. Molecular Physics.- World Scientific, 1997.- 772 p.].
В то время, когда писался обзор Гольдштейна, прямых измерений, способных непосредственно доказать условие прилипания, не было. В 1932 г. Фэдж и Тауненд с помощью ультрамикроскопа рассматривали турбулентное течение воды в канале квадратного сечения в непосредственной близости от стенки [Fage A., Townend H.C.H. An Examination of Turbulent Flow with an Ultramicroscope // Proc. R. Soc. Lond. A.- 1932.- Vol.135.- Pp.656-677]. По их оценкам самые медленные частицы двигались со скоростью 0.0018 м/с (среднерасходная скорость в канале составляла 0.253 м/с) на расстоянии от твердой поверхности 6.3×10-4 мм (630 нм). Причем последняя величина не измерялась, а определялась косвенным путем в предположении, что условие прилипания выполняется. Сам Гольдштейн признавал, что подобное экспериментальное свидетельство "едва ли можно считать самим по себе решающим" [Гольштейн С. Заметка об условиях на поверхности соприкосновения жидкости с твердым телом / Современное состояние гидроаэродинамики вязкой жидкости, т.2.- М.: Государственное издательство иностранной литературы, 1948.- С.356-361]. Показательно, что решающим аргументом в пользу условия прилипания ученый считал соображения, вытекающие из анализа размерностей.
Тем не менее, условие прилипания хорошо работало, и за сто лет к нему так привыкли, что стали считать чем-то само собой разумеющимся. Как сказано в одном известном учебнике по гидродинамике: "Другими словами, между жидкостью и твердой поверхностью относительного движения нет. Этот факт может удивлять, но он несомненно истинен. Не важно, насколько гладка твердая поверхность или насколько мала вязкость жидкости, - частицы, непосредственно прилегающие к стенке, не движутся относительно нее. Возможно небезынтересно, что Ньютон называл вязкость defectus lubricitatis - "потерей скользкости". Даже для жидкости, которая не "смачивает" поверхность, это правило не нарушается" [Massey B.S. Mechanics of Fluids.- London: Chapman and Hall, 1989.- 626 pp.].
Правда, было известно несколько специфических случаев, когда условие прилипания нарушалось:
В 1973 г. появилась важная работа Ричардсона [Richardson S. On the no-slip boundary condition // J. Fluid Mech.- 1973.- Vol.59.- No.4.- Pp.707-719], в которой была сделана попытка теоретически обосновать условие прилипания. Выбрав синусоидальную форму шероховатости стенки, он показал, что даже когда на микроскопическом уровне молекулы жидкости идеально скользят вдоль твердой поверхности, не встречая никакого сопротивления, на макроскопическом уровне реализуется условие прилипания. Логические аргументы Ричардсона кажутся безупречными. Некоторое сомнение вызывает правомерность применения его механической модели к явлениям на молекулярном уровне.
В таком контексте появление в последние годы большого числа (см. [Lauga E., Brenner M.P., Stone H.A. Microfluidics: The no-slip boundary condition / Springer Handbook of Experimental Fluid Mechanics (edited by Tropea C., Yarin A.L., Foss J.F.). Springer, 2007.- 1557 p.]) экспериментальных и численных работ, свидетельствующих о наличии кажущегося скольжения в ньютоновских жидкостях с длиной скольжения λ порядка от 1 до 1000 нм выглядит большой неожиданностью. Что это значит практически?
Конечно, речь не идет о том, что условие прилипания пора выбросить на свалку истории. Приведем некоторые выводы из обзора [Lauga E., Brenner M.P., Stone H.A. Microfluidics: The no-slip boundary condition / Springer Handbook of Experimental Fluid Mechanics (edited by Tropea C., Yarin A.L., Foss J.F.). Springer, 2007.- 1557 p.]:
Замечание 2. Не верно считать, что эффекты скольжения в ньютоновских жидкостях имеют значение только для микрогидродинамики. Так, например, в работе [Watanabe K., Udagawa Y., Udagawa H. Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall // J. Fluid Mech.- 1999.- Vol.381.- pp.225–238] был предложен остроумный метод снижения трения в трубе макроскопического размера посредством использования определенной шероховатости и "эффекта листа лотоса". Суть его в том, что жидкость при движении не только прилипает к твердой стенке, но и скользит по воздушной подушке между соседними элементами шероховатости, за счет чего уменьшается суммарное трение. Скольжению жидкости на супергидрофобной поверхности посвящен обзор [Rothstein J.P. Slip on Superhydrophobic Surfaces // Annu. Rev. Fluid Mech.- 2010.- Vol.42.- Pp.89-109].

Процессы, которые пытается описать условие прилипания/скольжения, выходят за рамки макроскопической гидродинамики. Речь здесь идет не столько о движении жидкости, сколько о межмолекулярном взаимодействии. На этом уровне нельзя говорить о жидкости как о сплошной неразрывной среде и описывать ее движение с помощью уравнений Навье-Стокса.
Необходимо отличать сложную физическую реальность взаимодействия молекул от простой макроскопической модели, которая используется для описания течения жидкости. Они могут вообще не соответствовать друг другу. С другой стороны, даже существенно противоречащие реальности модели могут давать правильные результаты (вспомним модель теплорода в работах С.Карно).
И условие прилипания и условие скольжения - лишь примитивные, грубые приближения к описанию очень сложных явлений. (Сравните прандтлевское определение границы турбулентного пограничного слоя по среднему профилю скорости и реальную границу в виде движущихся "языков" турбулентности на дымовых визуализациях.) В этом смысле оба они равно не верны, не адекватны, чрезмерно все упрощают и т.п. Какое из них использовать - решает практика научных исследований. Фактически, речь идет лишь о том или ином расчетном приеме.
Применять ту или иную гипотезу следует не "по традиции", не потому что "все так делают" или "мы верим (sic!), что это так", а потому что данное предположение приводит к меньшему числу противоречий с имеющимися экспериментальными свидетельствами. Нужно всегда быть готовым расстаться с привычной идеей, если она не выдерживает конкуренции с новыми/старыми моделями.
Для научного поиска важна терпимость к новым идеям. Большинство ключевых концепций в физике в момент их рождения казались ересью. Заблуждения в науке не менее важны, чем повторение общепринятых истин, потому что в спорах рождается свободная мысль.